pivoting
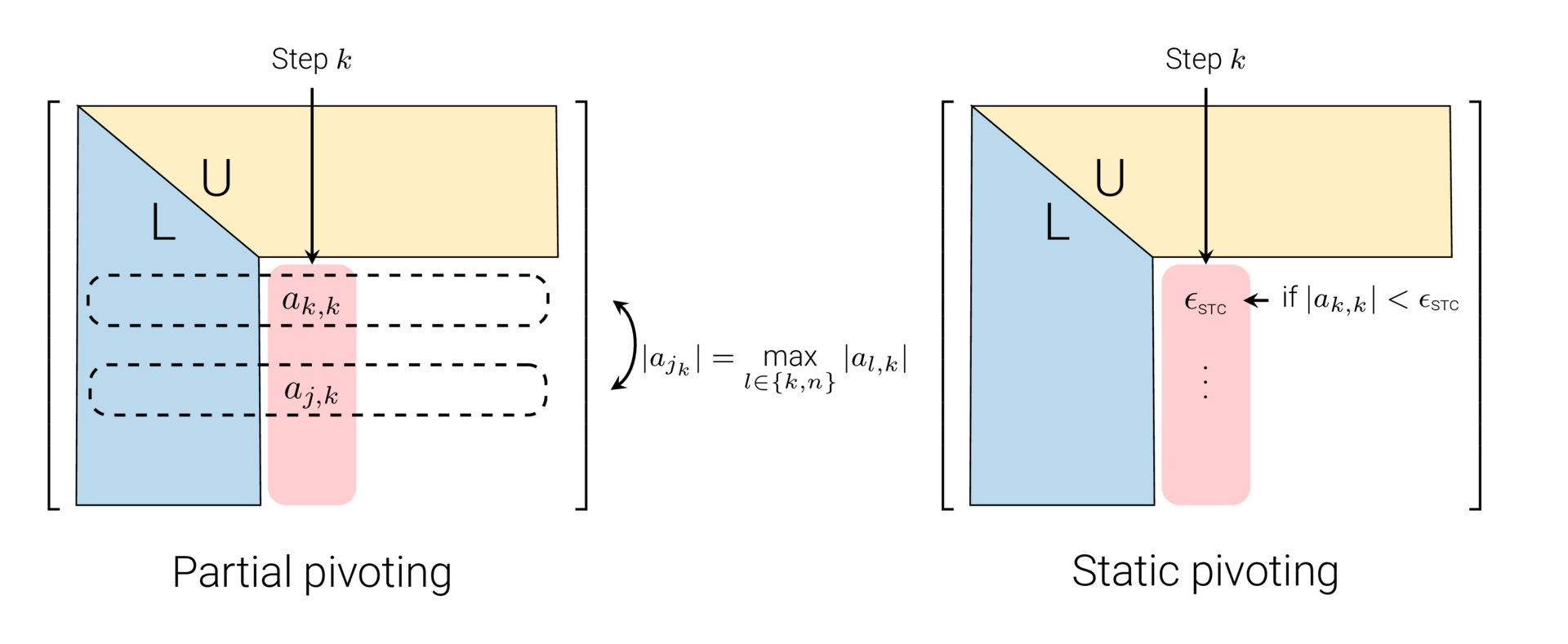
An illustration of partial and static pivoting.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
%%% Full, compilable sources are on Github:
%%% https://github.com/bvieuble/TeXFantasy/tree/main/illustrations/fig3
%%% Appears in my Ph.D. defense ``Mixed precision iterative refinement for the
%%% solution of large sparse linear systems''.
% Compiled with XeLaTeX
% TeX-command-extra-options: "-shell-escape"
\documentclass[convert={outext=.png},border=10pt]{standalone}
\usepackage{tikz}
\usetikzlibrary{matrix, positioning,fit,backgrounds,arrows.meta}
\input{color_theme.tex}
\begin{document}
\begin{tikzpicture}[>=stealth,thick,baseline]
\matrix [matrix of math nodes,left delimiter={[},right delimiter={]},
column sep=1mm, row sep=1mm,nodes={minimum width=.7cm,text depth=.14cm,
text height=.3cm}](A){
\phantom{a_{1,1}} & \phantom{a_{1,2}} & \phantom{a_{1,k}} & & &
\phantom{a_{1,6}} \\
\phantom{a_{2,1}} & \phantom{a_{2,2}} & \phantom{a_{2,k}} & & &
\phantom{a_{2,n}} \\
\phantom{a_{k,1}} & \phantom{a_{k,2}} & a_{k,k} & & & \phantom{a_{k,n}} \\
& & & & & \\
\phantom{a_{j,1}} & & a_{j,k} & & & \phantom{a_{j,n}} \\
\phantom{a_{n,1}} & \phantom{a_{n,2}} & \phantom{a_{n,3}} &
\phantom{a_{n,j}} & & \\
};
\node[right=15pt of A-3-6] (l1) {};
\node[right=15pt of A-5-6] (l2) {};
\node (L) at (A-2-1.east) {\Large L};
\node (U) at (A-1-2.south) {\Large U};
\node[above=5pt of A-1-3] (step) {\footnotesize Step $k$};
\node[fit=(A-3-1)(A-3-6),dashed,inner sep=-3pt,rounded corners=5pt,draw]
{};
\node[fit=(A-5-1)(A-5-6),dashed,inner sep=-3pt,rounded corners=5pt,draw]
{};
\path[<->] (l1.west) edge[bend left=55] node[name=max,right,near end]
{\footnotesize$|a_{j_k}|=\max\limits_{l\in\{k,n\}}|a_{l,k}|$}
(l2.west);
\path[->] (step) edge (A-3-3);
\begin{scope}[on background layer]
\draw[fill=myblue-light] (A-1-1.north west) -- (A-6-1.south west) --
(A-6-2.south east) -- (A-2-2.south east) -- cycle;
\draw[fill=myyellow-light] (A-1-1.north west) -- (A-1-6.north east) --
(A-2-6.south east) -- (A-2-2.south east) -- cycle;
\node[fit=(A-3-3)(A-6-3),inner sep=0pt,fill=myred-light,
rounded corners=5pt] {};
\end{scope}
\node[below=10pt of A-6-3] (title) {\large Partial pivoting};
\end{tikzpicture}
\begin{tikzpicture}[>=stealth,thick,baseline]
\matrix [matrix of math nodes,left delimiter={[},right delimiter={]},
column sep=1mm, row sep=1mm,nodes={minimum width=.7cm,text depth=.14cm,
text height=.3cm}](A){
\phantom{a_{1,1}} & \phantom{a_{1,2}} & & & & \phantom{a_{1,6}} \\
\phantom{a_{2,1}} & \phantom{a_{2,2}} & \phantom{a_{2,k}} & & &
\phantom{a_{2,n}} \\
\phantom{a_{k,1}} & \phantom{a_{k,2}} & \epsilon_{\mbox{\tiny
\textsc{stc}}} & & & \phantom{a_{k,n}} \\
& & & & & \\
\phantom{a_{j,1}} & & \vdots & & & \phantom{a_{j,n}} \\
\phantom{a_{n,1}} & \phantom{a_{n,2}} & \phantom{a_{n,3}} &
\phantom{a_{n,j}} & & \\
};
\node[right=15pt of A-3-6] (l1) {};
\node[right=15pt of A-5-6] (l2) {};
\node[above=5pt of A-1-3] (step) {\footnotesize Step $k$};
\node[right=7pt of A-3-3] (tau) {\footnotesize if $|a_{k,k}|<
\epsilon_{\mbox{\tiny \textsc{stc}}}$};
\node (L) at (A-2-1.east) {\Large L};
\node (U) at (A-1-2.south) {\Large U};
\path[->] (tau) edge (A-3-3);
\path[->] (step) edge (A-3-3);
\begin{scope}[on background layer]
\draw[fill=myblue-light] (A-1-1.north west) -- (A-6-1.south west) --
(A-6-2.south east) -- (A-2-2.south east) -- cycle;
\draw[fill=myyellow-light] (A-1-1.north west) -- (A-1-6.north east) --
(A-2-6.south east) -- (A-2-2.south east) -- cycle;
\node[fit=(A-3-3)(A-6-3),inner sep=0pt,fill=myred-light,
rounded corners=5pt] {};
\end{scope}
\node[below=10pt of A-6-3] (title) {\large Static pivoting};
\end{tikzpicture}
\end{document}