floating-point (copy)
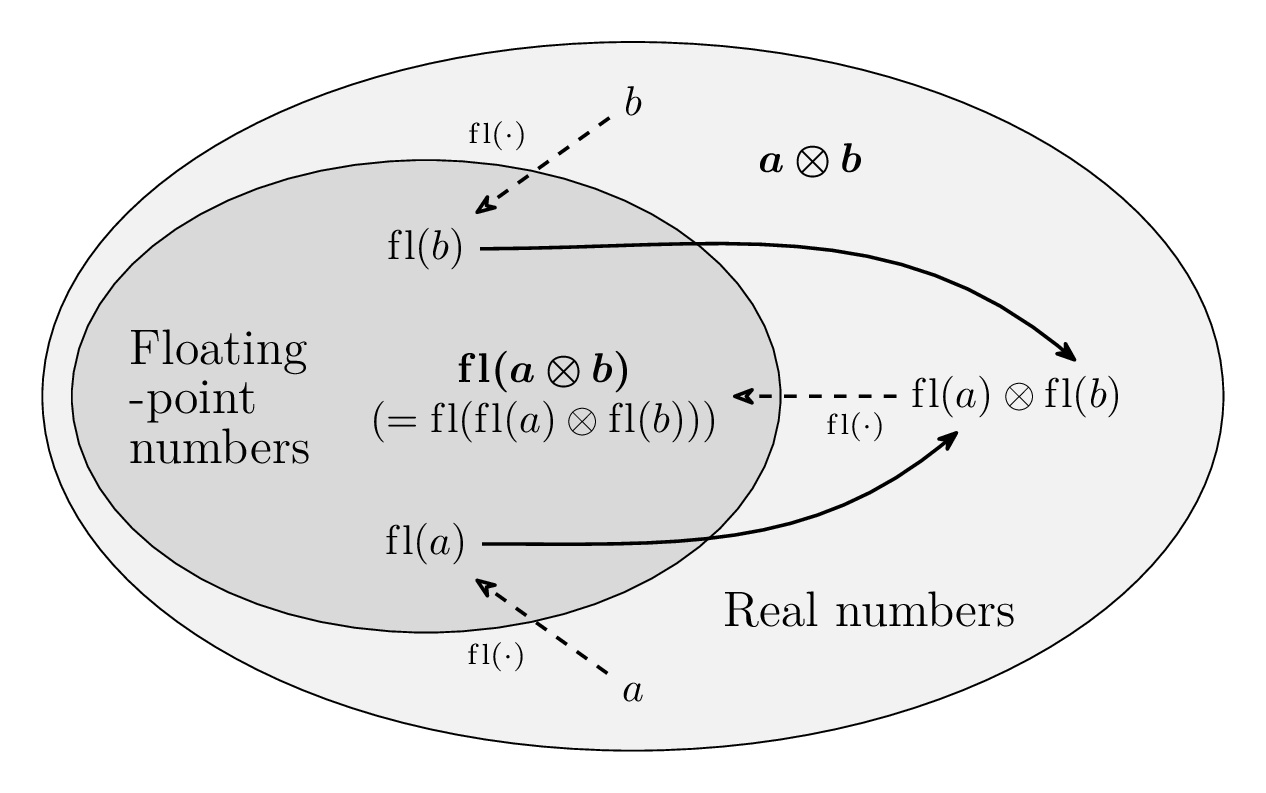
An illustration explaining floating-point computation.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
%%% Compiled with XeLaTeX
%%% TeX-command-extra-options: "-shell-escape"
%%% Original illustration in: https://jasss.soc.surrey.ac.uk/9/4/4.html
\documentclass[convert={outext=.png},border=10pt]{standalone}
% \usepackage{fontspec}
% \setmainfont{Roboto Light}
\usepackage{tikz}
\usetikzlibrary{calc,positioning,shapes.geometric,arrows.meta}
\usepackage{amsmath}
\usepackage{amssymb}
\usepackage{bm}
\DeclareMathOperator{\fl}{\operatorname{f\kern.2ptl}}
\input{color_theme.tex}
\begin{document}
\begin{tikzpicture}
\draw[fill=gray!10] (0,0) ellipse (5 and 3);
\draw[fill=gray!30] (-1.75,0) ellipse (3 and 2);
\node[align=left] at (2,-1.8) {\large Real numbers};
\node[align=left] at (-3.5,0)
{\large Floating\\\large -point\\\large numbers};
\node[align=center] (fla) at (-1.75,-1.25) {$\fl(a)$};
\node[align=center] (a) at (0,-2.5) {$a$};
\path[-{Stealth[open,round]},dashed,thick] (a) edge node[below left]
{\scriptsize $\fl(\cdot)$} (fla);
\node[align=center] (flb) at (-1.75,1.25) {$\fl(b)$};
\node[align=center] (b) at (0,2.5) {$b$};
\path[-{Stealth[open,round]},dashed,thick] (b) edge node[above left]
{\scriptsize $\fl(\cdot)$} (flb);
\node[align=center] (flab) at (3.25,0) {$\fl(a) \otimes \fl(b)$};
\path[-{Stealth[round]},thick] (fla) edge [out=0, in=-140]
($(flab)+(-0.5,-0.3)$);
\path[-{Stealth[round]},thick] (flb) edge [out=0, in=140]
($(flab)+(0.5,0.3)$);
\node[align=center] (flflab) at (-0.75,0) {$\bm{\fl(a \otimes b)}$ \\
$(=\fl(\fl(a) \otimes \fl(b)))$};
\path[-{Stealth[open,round]},dashed,thick] (flab) edge
node[below,near start] {\scriptsize $\fl(\cdot)$} (flflab);
\node[align=center] (ab) at (1.5,2) {$\bm{a\otimes b}$};
\end{tikzpicture}
\end{document}